Công Thức Lượng Giác là “bộ công cụ” giúp bạn biến đổi biểu thức, rút gọn, chứng minh đẳng thức và giải phương trình lượng giác một cách có hệ thống. Nếu học theo kiểu ghi nhớ rời rạc, bạn rất dễ nhầm dấu, nhầm điều kiện hoặc áp dụng sai ngữ cảnh, đặc biệt ở các bài cần biến đổi nhiều bước. Vì vậy, cách học hiệu quả là hiểu cấu trúc công thức theo nhóm và luyện dùng đúng “điểm rơi” trong từng dạng bài.
Trong bài viết này, bạn sẽ thấy các nhóm công thức quan trọng nhất: cơ bản (liên hệ sin, cos, tan, cot), cộng–trừ, nhân đôi–nửa góc, hạ bậc, tổng–tích, cùng một quy trình chọn công thức để làm bài nhanh và chắc.
Công Thức Lượng Giác là gì và vì sao phải nắm chắc?
Công Thức Lượng Giác là tập hợp các đẳng thức liên hệ giữa sin, cos, tan, cot của các góc khác nhau (a, b, 2a, a/2, …) nhằm phục vụ biến đổi đại số. Điểm quan trọng là mọi biến đổi phải giữ đúng điều kiện xác định, ví dụ tan x chỉ tồn tại khi cos x ≠ 0. Khi hiểu bản chất này, bạn sẽ tránh được lỗi “rút gọn cho 0” hoặc biến đổi làm mất nghiệm.
Ở cấp THPT, các công thức không chỉ để “thay số tính nhanh” mà chủ yếu để rút gọn biểu thức và đưa bài toán về dạng quen thuộc. Nhiều câu phân loại yêu cầu nhận ra cấu trúc như sin a cos b hoặc cos a ± cos b để đổi sang tổng–tích (hoặc tích–tổng). Nếu bạn nhận diện đúng cấu trúc ngay từ đầu, lời giải thường ngắn hơn đáng kể.
Khi nào nên ưu tiên biến đổi thay vì bấm máy?
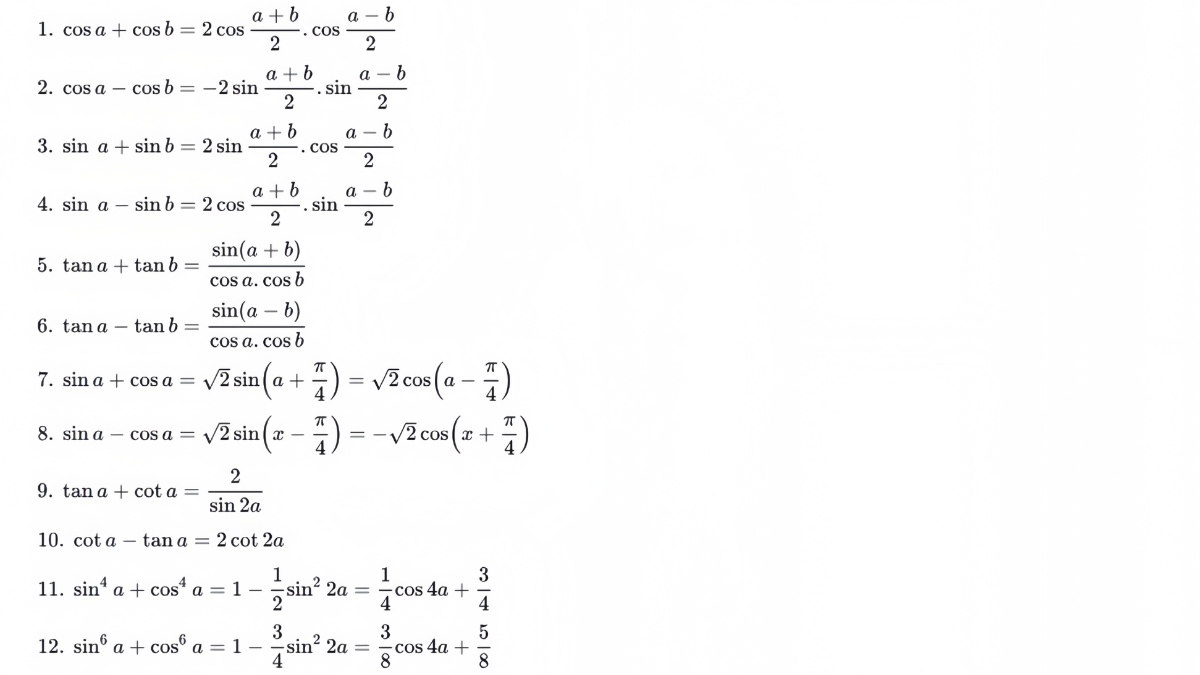
Trong bài rút gọn và chứng minh, ưu tiên biến đổi vì máy tính không kiểm soát được điều kiện và không thay thế được lập luận. Ngay cả khi đề cho giá trị cụ thể, việc biến đổi vẫn giúp bạn “đóng khung” biểu thức về các dạng chuẩn như sin²x + cos²x, hoặc 1 + tan²x. Khi đó, bạn kiểm soát được dấu và miền giá trị, giảm rủi ro ra đáp án sai do làm tắt.
Trong bài giải phương trình, biến đổi đúng giúp bạn đưa về phương trình cơ bản theo sin x hoặc cos x, hoặc chuyển sang tan(x/2) để giải gọn. Cách làm này đặc biệt hữu ích khi phương trình chứa cả sin x và cos x lẫn bậc hai. Bạn nên tập thói quen ghi điều kiện xác định ngay từ dòng đầu, vì đó là “hàng rào” bảo vệ nghiệm cùng Công Thức Lượng Giác.
Công thức cơ bản của sin, cos, tan, cot
Ở nhóm nền tảng, bạn cần thuộc các hệ thức Pythagore và hệ thức giữa tan, cot với sin, cos. Những công thức này xuất hiện dày đặc trong mọi dạng bài và thường là bước rút gọn cuối cùng để “khóa” kết quả. Thực hành nhiều sẽ giúp bạn nhìn thấy ngay cách đưa phân thức về dạng 1 ± cos x hoặc 1 + tan²x.
Các hệ thức cơ bản tiêu biểu:
\(\sin^2 x + \cos^2 x = 1\)
\(\tan x = \frac{\sin x}{\cos x}\quad(\cos x \ne 0),\qquad \cot x = \frac{\cos x}{\sin x}\quad(\sin x \ne 0)\)
\(1+\tan^2 x=\frac{1}{\cos^2 x}\quad(\cos x \ne 0),\qquad 1+\cot^2 x=\frac{1}{\sin^2 x}\quad(\sin x \ne 0)\)
Mẹo nhận diện nhanh để rút gọn phân thức
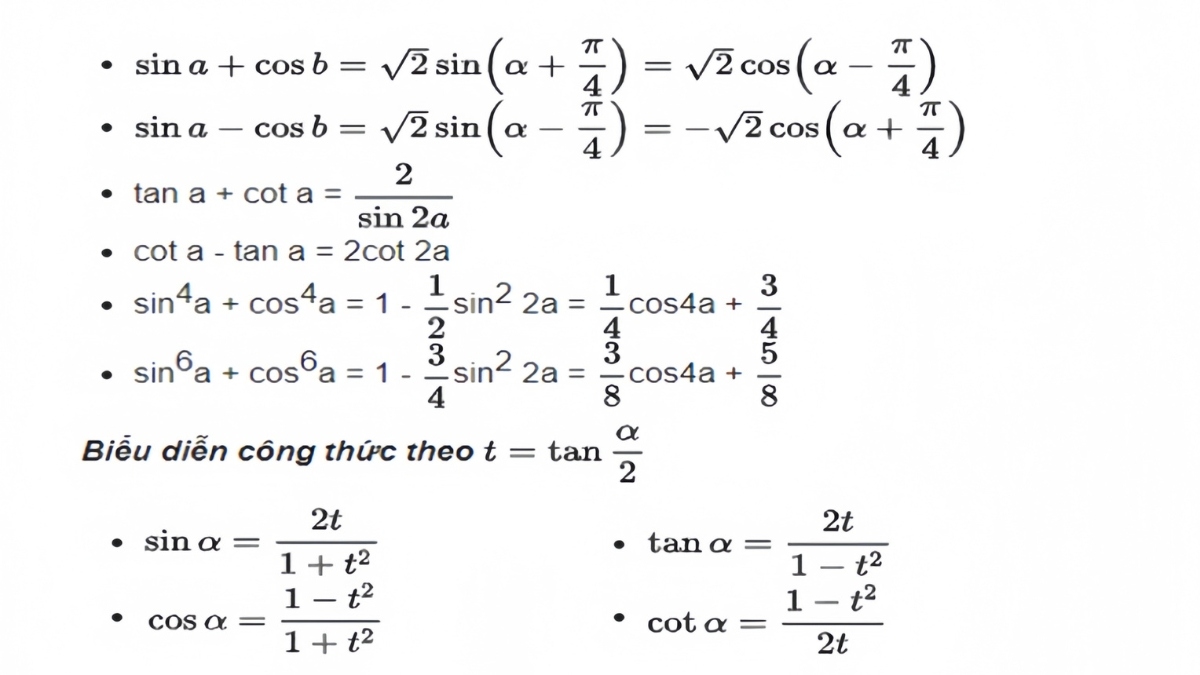
Khi gặp biểu thức kiểu (\dfrac{\sin2 x}{1-\cos x}), bạn nên nghĩ đến nhân liên hợp hoặc đổi (\sin2 x = 1-\cos^2 x) để triệt tiêu. Nếu thấy (\dfrac{1-\cos x}{\sin x}), thường có thể quy về (\tan(x/2)) bằng công thức nửa góc. Tư duy “nhìn mẫu đoán công thức” giúp tiết kiệm rất nhiều thời gian so với việc biến đổi ngẫu nhiên.
Một nguyên tắc an toàn là ưu tiên đưa về sin và cos trước, rồi mới đổi sang tan/cot nếu cần. Tan và cot giúp rút gọn nhanh khi biểu thức là phân thức theo sin, cos, nhưng cũng dễ phát sinh điều kiện xác định. Vì vậy, bạn chỉ nên chuyển sang tan/cot khi chắc chắn kiểm soát được miền xác định.
Công thức cộng và trừ góc
Nhóm cộng–trừ là nền tảng để mở rộng biểu thức có hai góc và cũng là “cửa vào” cho tổng–tích. Công Thức Lượng Giác ở nhóm này thường được dùng để khai triển sin(a±b), cos(a±b) hoặc biến đổi ngược để gom nhóm. Bạn cần thuộc chính xác dấu trong công thức cos(a±b), vì đây là nơi học sinh hay sai nhất.
Các công thức chuẩn:
\(\sin(a\pm b)=\sin a\cos b \pm \cos a\sin b\)
\(\cos(a\pm b)=\cos a\cos b \mp \sin a\sin b\)
\(\tan(a\pm b)=\frac{\tan a \pm \tan b}{1 \mp \tan a\tan b}\quad(\text{điều kiện mẫu }\ne 0)\)
Ứng dụng: gom hạng và nhận diện cấu trúc
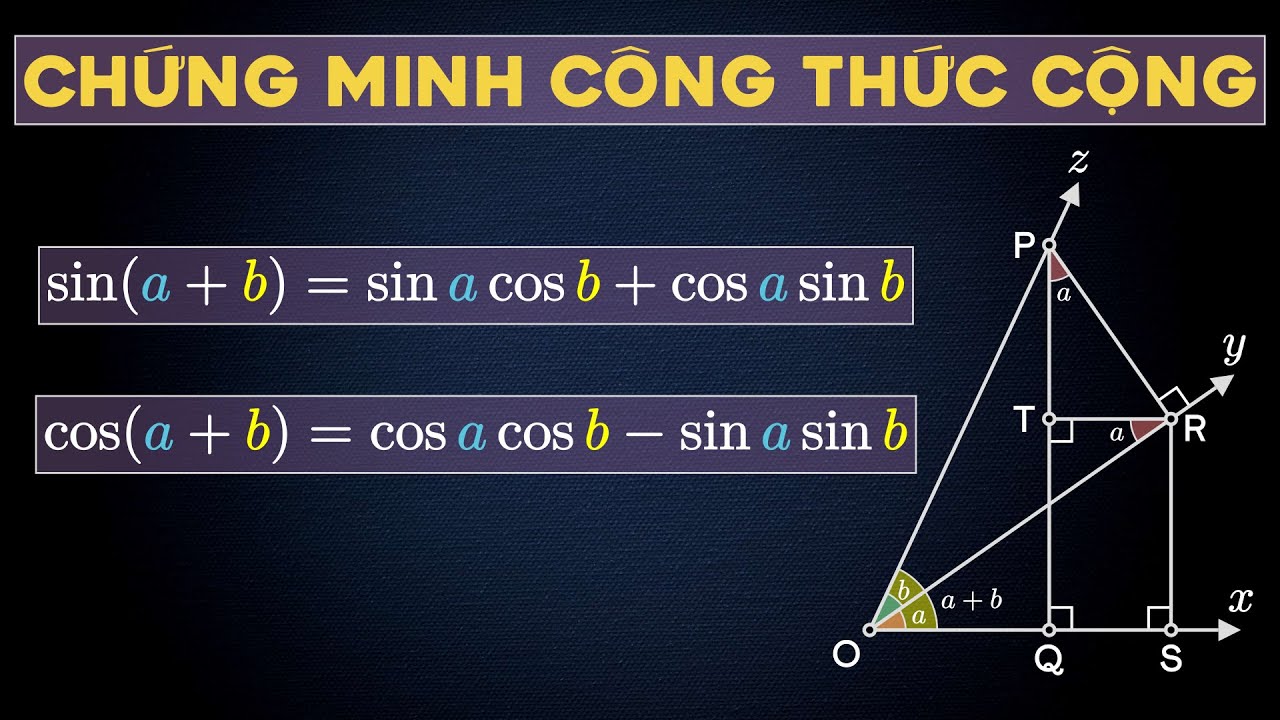
Khi thấy dạng (\sin a\cos b + \cos a\sin b), bạn nên nhận ra đó chính là (\sin(a+b)). Tương tự, (\cos a\cos b + \sin a\sin b) là (\cos(a-b)), còn (\cos a\cos b – \sin a\sin b) là (\cos(a+b)). Chỉ cần đổi “một cặp” đúng, biểu thức có thể rút gọn ngay về một hàm lượng giác đơn.
Trong bài chứng minh, bạn nên biến đổi về một vế bằng cách đưa mọi thứ về sin và cos Công Thức Lượng Giác, rồi dùng cộng–trừ để gom lại thành sin(a±b) hoặc cos(a±b). Cách làm này thường sạch sẽ hơn so với việc biến đổi cả hai vế song song. Cuối cùng, hãy luôn kiểm tra điều kiện nếu bạn có dùng công thức của tan.
Công thức nhân đôi, nhân ba và nửa góc
Nhóm nhân đôi và nửa góc giúp bạn xử lý góc 2x, x/2 hoặc đưa bậc của sin, cos về dạng thuận tiện. Đây cũng là nhóm hay được dùng trong bài tính giá trị biểu thức khi biết một trong các giá trị sin x, cos x, tan x. Bạn không nhất thiết phải thuộc quá nhiều biến thể, nhưng nên nắm các dạng “cốt lõi” và biết chuyển đổi linh hoạt giữa chúng.
Công thức nhân đôi:
\(\sin 2x=2\sin x\cos x\)
\(\cos 2x=\cos^2 x-\sin^2 x=2\cos^2 x-1=1-2\sin^2 x\)
\(\tan 2x=\frac{2\tan x}{1-\tan^2 x}\quad(\cos x\ne 0,\ 1-\tan^2 x\ne 0)\)
Nửa góc và liên hệ với tan(x/2)
Khi gặp (1\pm \cos x) hoặc biểu thức chứa (\sin x) ở mẫu, bạn nên cân nhắc dùng nửa góc. Các công thức thường dùng:
\(\sin^2\frac{x}{2}=\frac{1-\cos x}{2},\qquad \cos^2\frac{x}{2}=\frac{1+\cos x}{2}\)
\(\tan\frac{x}{2}=\frac{\sin x}{1+\cos x}=\frac{1-\cos x}{\sin x}\quad(\text{điều kiện mẫu }\ne 0)\)
Kỹ thuật tan(x/2) đặc biệt mạnh khi giải phương trình có cả sin x và cos x ở dạng phân thức. Tuy nhiên, bạn phải ghi rõ điều kiện như (\sin x \ne 0) hoặc (1+\cos x \ne 0) tùy biến thể, để tránh đưa vào nghiệm ngoại lai. Nếu kiểm soát điều kiện tốt, phương pháp này thường cho lời giải gọn và nhất quán.
Công thức hạ bậc và biến đổi tổng–tích
Ở các bài rút gọn biểu thức có (\sin2 x, \cos2 x, \sin x\cos x), hạ bậc giúp bạn đưa về góc 2x để gom nhóm. Đây là cách điển hình để xử lý các biểu thức bậc cao mà không cần khai triển dài. Nhiều bài còn yêu cầu đổi tổng thành tích hoặc tích thành tổng để tiện tính toán hoặc chứng minh.
Công thức hạ bậc:
\(\sin^2 x=\frac{1-\cos 2x}{2},\qquad \cos^2 x=\frac{1+\cos 2x}{2}\)
\(\sin x\cos x=\frac{\sin 2x}{2}\)
Tổng–tích và tích–tổng: dùng đúng tình huống
Khi đề cho biểu thức dạng (\sin a + \sin b) hoặc (\cos a – \cos b), bạn nên đổi sang tích để dễ rút gọn:
\(\sin a+\sin b=2\sin\frac{a+b}{2}\cos\frac{a-b}{2}\)
\(\sin a-\sin b=2\cos\frac{a+b}{2}\sin\frac{a-b}{2}\)
\(\cos a+\cos b=2\cos\frac{a+b}{2}\cos\frac{a-b}{2}\)
\(\cos a-\cos b=-2\sin\frac{a+b}{2}\sin\frac{a-b}{2}\)
Ngược lại, nếu bạn gặp tích như (\sin a\cos b), đổi sang tổng sẽ hữu ích để “gom” về dạng cộng–trừ góc:
\(\sin a\cos b=\frac{1}{2}\left[\sin(a+b)+\sin(a-b)\right]\)
\(\cos a\cos b=\frac{1}{2}\left[\cos(a+b)+\cos(a-b)\right]\)
\(\sin a\sin b=\frac{1}{2}\left[\cos(a-b)-\cos(a+b)\right]\)
Quy trình chọn công thức để làm bài nhanh và chắc
Công Thức Lượng Giác sẽ phát huy hiệu quả nhất khi bạn có quy trình ra quyết định rõ ràng, thay vì “thử từng công thức”. Bước đầu tiên là phân loại: rút gọn, chứng minh, tính giá trị hay giải phương trình. Bước thứ hai là nhận diện cấu trúc: tổng/hiệu, tích, góc đôi, bậc hai, hoặc phân thức có 1±cos x. Từ cấu trúc đó, bạn chọn nhóm công thức tương ứng và ưu tiên biến đổi theo hướng làm giảm số hạng hoặc giảm bậc.
Một nguyên tắc thực dụng là luôn hướng biểu thức về các “đích” quen thuộc như (\sin2 x+\cos2 x), (\cos 2x), (\sin 2x) hoặc (\tan(x/2)). Sau mỗi bước biến đổi, bạn nên kiểm tra xem biểu thức đã đơn giản hơn chưa; nếu dài hơn và không có dấu hiệu triệt tiêu, hãy dừng lại và đổi hướng. Thói quen này giúp bạn tránh sa đà vào biến đổi lan man.
Ví dụ mẫu: rút gọn một biểu thức thường gặp
Xét (A=\dfrac{1-\cos 2x}{\sin 2x}) với điều kiện (\sin 2x\ne 0). Bạn có thể dùng hạ bậc và nhân đôi để đưa về nửa góc. Vì (1-\cos 2x=2\sin2 x) và (\sin 2x=2\sin x\cos x), suy ra (A=\dfrac{2\sin2 x}{2\sin x\cos x}=\dfrac{\sin x}{\cos x}=\tan x), đồng thời giữ điều kiện (\cos x\ne 0). Cách làm này ngắn vì bạn chọn đúng công thức làm xuất hiện triệt tiêu ngay ở bước kế tiếp.
Trong các bài tương tự, nếu mẫu là (\sin 2x) hoặc (\cos 2x), bạn nên nghĩ đến công thức nhân đôi trước tiên. Nếu tử là (1\pm\cos 2x), hạ bậc thường là lựa chọn tối ưu. Điều quan trọng là luôn ghi điều kiện xác định để kết luận cuối cùng không bị thiếu chặt chẽ.
Lỗi thường gặp và cách tự luyện hiệu quả
Lỗi phổ biến nhất là nhầm dấu ở (\cos(a\pm b)) hoặc đổi tổng–tích sai “dấu trừ”. Bạn nên luyện theo thói quen kiểm tra nhanh bằng một giá trị đặc biệt, chẳng hạn cho (b=0) để xem công thức có khớp (\sin(a+0)=\sin a) hay không. Cách kiểm tra này không thay thế chứng minh, nhưng rất hiệu quả để phát hiện nhầm dấu trước khi đi quá xa cùng với mua Vape.
Để luyện tốt, bạn nên chia bài tập theo nhóm công thức và đặt mục tiêu rõ ràng: mỗi ngày rút gọn 5 biểu thức dùng hạ bậc, 5 biểu thức dùng tổng–tích, và 2 phương trình dùng tan(x/2). Sau khi làm xong, hãy tự viết lại “tín hiệu nhận diện” cho từng nhóm, ví dụ thấy (\sin a\cos b) là nghĩ đến tích–tổng. Luyện đều như vậy, bạn sẽ hình thành phản xạ chọn công thức nhanh và chính xác.
