Chu Vi Hình Tròn là độ dài của đường bao tròn, được dùng liên tục trong học tập lẫn đo đạc thực tế. Nắm chắc công thức và cách kiểm tra giúp bạn tính đúng kích thước vòng ngoài của bánh xe, nắp hộp, ống tròn hay chi tiết kỹ thuật.
Chu Vi Hình Tròn là gì và vì sao quan trọng?
Khái niệm chu vi đối với hình tròn
Chu vi là tổng độ dài đường biên của một hình phẳng. Với hình tròn, đường biên chính là đường tròn cách đều tâm một khoảng không đổi, nên Chu Vi Hình Tròn luôn được đo bằng đơn vị độ dài như mm, cm hoặc m. Tính “đều” này giúp một đường cong tưởng khó đo trở thành đại lượng có thể tính toán ổn định.
Tầm quan trọng trong đo lường và mô hình hóa
Trong lớp học, chu vi là cầu nối giữa hình học và đại số thông qua hằng số π. Trong thực tế, chu vi thường là dữ liệu đầu vào để ước tính vật liệu bao quanh, quãng đường đi được sau một vòng quay, hoặc kích thước cần cắt, dán, uốn. Vì vậy, hiểu đúng khái niệm và kiểm soát sai số là điều bắt buộc khi chuyển từ bài tập sang ứng dụng cùng Chu Vi Hình Tròn.
Công thức tính chu vi và cách áp dụng
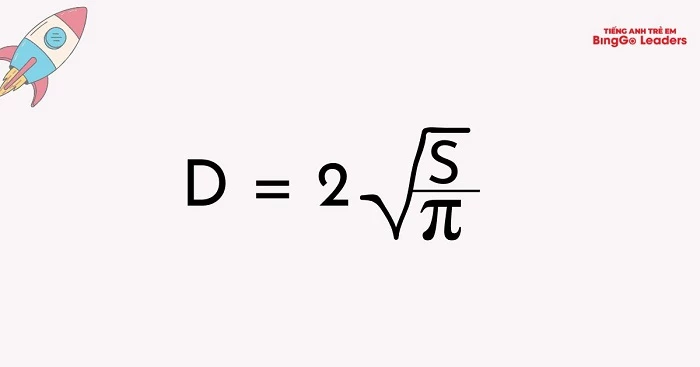
Công thức chuẩn và dạng tương đương
Công thức cơ bản là C = 2πr, trong đó r là bán kính và π ≈ 3,14159. Nếu dùng đường kính d = 2r, bạn có thể viết gọn C = πd, tiện khi đo trực tiếp bề ngang của hình tròn. Dù dùng dạng nào, hãy đảm bảo các đại lượng cùng hệ đơn vị trước khi tính.
Cách thay số nhanh và ví dụ ngắn
Một quy trình gọn gồm ba bước: xác định r hoặc d; chọn mức làm tròn của π (3,14; 3,1416; hoặc dùng phím π); nhân theo công thức và ghi đơn vị. Ví dụ r = 7 cm thì C = 2 × π × 7 ≈ 43,98 cm (π = 3,1416), làm tròn thành 44,0 cm nếu đề bài yêu cầu đến 0,1 cm cùng Chu Vi Hình Tròn. Để tự kiểm tra, nhớ rằng chu vi xấp xỉ 3,14 lần đường kính, nên kết quả “quá xa” mức này thường là dấu hiệu nhầm biến.
Lịch sử và ý nghĩa của số π
Từ xấp xỉ cổ đại đến phương pháp của Archimedes
Nhiều nền văn minh cổ đã nhận ra tỉ số giữa chu vi và đường kính gần như không đổi, từ đó đưa ra các xấp xỉ của π để phục vụ xây dựng và đo đạc. Archimedes phát triển cách “kẹp” π bằng đa giác nội tiếp và ngoại tiếp, cho ra các cận trên dưới sát giá trị thật. Tư duy xấp xỉ này về sau trở thành nền tảng cho việc đánh giá sai số trong toán học và kỹ thuật.
Vì sao π xuất hiện ở mọi đường tròn
Điều làm π đặc biệt là tính phổ quát: mọi đường tròn, dù lớn hay nhỏ, đều có tỉ số C/d giống nhau. Khi toán học phát triển, π còn xuất hiện trong chuỗi vô hạn và tích phân, cho thấy đây là một hằng số cấu trúc chứ không chỉ là “con số để nhớ”. Vì thế, công thức chu vi được chuẩn hóa rộng rãi và dùng như viên gạch đầu tiên để mở rộng sang cung tròn và chuyển động tròn.
Vai trò trong học tập và ứng dụng kỹ thuật
Rèn tư duy tỉ lệ, đơn vị và suy luận ngược
Tính chu vi buộc người học phân biệt bán kính với đường kính, đồng thời giữ nhất quán đơn vị trước khi thay số. Bạn cũng thấy rõ tính tuyến tính: bán kính tăng gấp đôi thì chu vi tăng gấp đôi, giúp kiểm tra nhanh tính hợp lý của kết quả. Ngoài ra, việc suy luận ngược từ chu vi ra bán kính (r = C/(2π)) là kỹ năng hữu ích khi dữ kiện đến từ đo đạc thực tế Chu Vi Hình Tròn.
Ứng dụng trong đời sống, sản xuất và cơ khí
Trong thiết kế bao bì, chu vi quyết định chiều dài nhãn quấn quanh lon hoặc chai, nên lệch nhỏ cũng có thể gây hở mép hoặc nhăn. Trong cơ khí, chu vi bánh xe liên quan trực tiếp quãng đường đi được sau mỗi vòng quay, từ đó suy ra tốc độ khi biết số vòng quay theo thời gian. Trong xây dựng và gia công, chu vi hỗ trợ ước lượng vật liệu viền, đai, vòng đệm và giúp giảm sai số khi lắp ghép.
Sai lầm thường gặp và mẹo kiểm tra
Nhầm bán kính với đường kính
Lỗi phổ biến nhất là lấy đường kính thay cho bán kính trong C = 2πr, khiến kết quả lớn gấp đôi. Cách phòng tránh là ghi rõ “r = …” hoặc “d = …” ngay dưới dữ kiện, rồi chọn công thức tương ứng. Bạn cũng có thể ước lượng bằng C ≈ 3,14d để phát hiện nhanh những kết quả “bất thường”.
Làm tròn π quá sớm và đổi đơn vị thiếu nhất quán
Nếu làm tròn π quá thô ngay từ bước đầu, sai số sẽ tăng theo kích thước và có thể vượt ngưỡng chấp nhận trong kỹ thuật. Hãy giữ π nhiều chữ số khi tính trung gian, rồi mới làm tròn ở bước cuối theo yêu cầu. Đồng thời, đừng trộn lẫn mm, cm và m trong cùng phép tính; đổi đơn vị một lần rõ ràng sẽ giúp kết quả dễ kiểm tra và ít nhầm hơn cùng với sieuthivape.
Kết luận
Ghi nhớ nhanh để dùng đúng
Khi cần tính độ dài vòng ngoài, hãy xác định đúng r hoặc d, chọn mức làm tròn phù hợp và kiểm tra bằng ước lượng theo đường kính. Chu Vi Hình Tròn được tóm gọn trong C = 2πr hoặc C = πd, nhưng điều quan trọng là bạn biết dùng đúng biến và quản lý sai số theo bối cảnh. Thực hành vài bài suy luận ngược sẽ giúp bạn áp dụng công thức này nhanh và chắc trong cả học tập lẫn công việc.
