Bảng Đạo Hàm là “phao cứu sinh” khi bạn cần tra nhanh công thức trong lúc học giải tích, làm bài kiểm tra hoặc ôn thi. Bảng Đạo Hàm giúp bạn tiết kiệm thời gian ghi nhớ rời rạc, đồng thời giảm sai sót khi xử lý biểu thức phức tạp. Nếu biết kết hợp bảng với các quy tắc đạo hàm, bạn sẽ tính nhanh hơn và kiểm tra kết quả cũng chắc chắn hơn.
Bảng Đạo Hàm: Khái niệm và phạm vi áp dụng
Tại sao nên dùng bảng khi học đạo hàm
Trong chương trình phổ thông và đại cương, nhiều bài toán yêu cầu tính đạo hàm lặp đi lặp lại theo cùng một “mẫu” công thức. Bảng Đạo Hàm cung cấp các dạng hàm số chuẩn để bạn đối chiếu ngay lập tức, từ đó tập trung thời gian cho phần biến đổi và áp dụng quy tắc. Khi luyện đề, việc tra nhanh còn giúp bạn duy trì nhịp làm bài và hạn chế mất điểm vì nhầm dấu.
Cách đọc ký hiệu và điều kiện xác định
Bạn sẽ gặp các ký hiệu như \(y’\), \(\dfrac{dy}{dx}\) hoặc \(f'(x)\), tất cả đều diễn tả tốc độ thay đổi của hàm theo biến \(x\). Bảng Đạo Hàm thường giả định hàm số xác định trên miền hợp lệ, nên bạn cần tự kiểm tra điều kiện như \(x>0\) với \(\ln x\) hoặc \(|x|<1\) với \(\arcsin x\). Việc kiểm tra điều kiện trước khi kết luận giúp tránh lỗi “đúng công thức nhưng sai miền”.
Quy tắc tính đạo hàm nền tảng
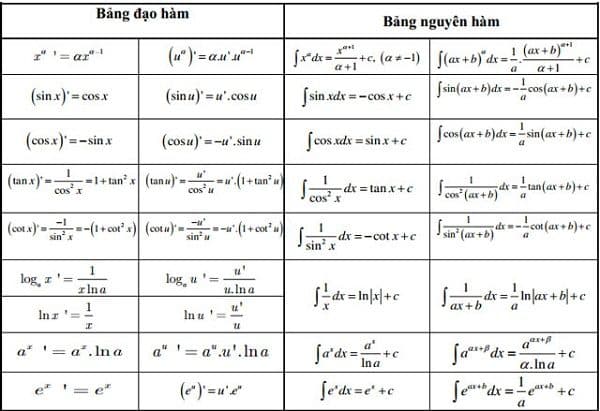
Quy tắc tuyến tính và biến đổi cơ bản
Đạo hàm của tổng/hiệu bằng tổng/hiệu các đạo hàm, và hệ số nhân có thể đưa ra ngoài: \((af(x))’ = a f'(x)\). Bảng Đạo Hàm chỉ phát huy hiệu quả tối đa khi bạn tách biểu thức thành các phần “nhìn ra” dạng quen thuộc, thay vì cố đạo hàm nguyên khối. Thói quen rút gọn, phân tích nhân tử và quy đồng trước khi đạo hàm thường giúp bài toán ngắn gọn hơn.
Tích, thương và dây chuyền
Khi gặp tích \(u\cdot v\), dùng \((uv)’ = u’v + uv’\), còn thương \(\dfrac{u}{v}\) dùng \(\left(\dfrac{u}{v}\right)’=\dfrac{u’v-uv’}{v^2}\). Bảng Đạo Hàm không thay thế quy tắc dây chuyền, vì với hàm hợp \(y=f(g(x))\) bạn cần \(y’ = f'(g(x))\cdot g'(x)\). Nắm chắc dây chuyền là chìa khóa để xử lý các dạng như \((\sin(3x-1))’\) hoặc \(\ln(x^2+1)’\).
Bảng đạo hàm cơ bản cho hàm đại số
Hàm hằng, bậc nhất và lũy thừa
Các hàm đại số là phần xuất hiện dày đặc nhất trong bài tập, đặc biệt khi kết hợp với quy tắc nhân và dây chuyền. Bảng Đạo Hàm dưới đây tóm tắt các công thức cốt lõi để bạn có thể nhận dạng nhanh và thay thế đúng dạng. Khi áp dụng, hãy chú ý phân biệt \(x^n\) với \((ax+b)^n\) để dùng dây chuyền cho chính xác.
| Hàm số \(y\) | Đạo hàm \(y’\) |
|---|---|
| \(c\) (hằng số) | \(0\) |
| \(x\) | \(1\) |
| \(x^n\) (với \(n\in\mathbb{R}\)) | \(n x^{n-1}\) |
| \(\dfrac{1}{x}=x^{-1}\) | \(-\dfrac{1}{x^2}\) |
Căn thức và phân thức thường gặp

Căn thức có thể viết lại dưới dạng lũy thừa để áp dụng công thức nhanh, ví dụ \(\sqrt{x}=x^{1/2}\). Bảng Đạo Hàm sẽ hiệu quả hơn nếu bạn ưu tiên “chuẩn hóa” biểu thức trước, chẳng hạn đổi \(\dfrac{\sqrt{x}}{x}\) thành \(x^{-1/2}\). Với phân thức, hãy cân nhắc rút gọn trước khi dùng quy tắc thương để giảm rủi ro sai dấu.
| Hàm số \(y\) | Đạo hàm \(y’\) |
|---|---|
| \(\sqrt{x}=x^{1/2}\) | \(\dfrac{1}{2\sqrt{x}}\) |
| \(\dfrac{1}{\sqrt{x}}=x^{-1/2}\) | \(-\dfrac{1}{2x^{3/2}}\) |
| \(\sqrt[n]{x}=x^{1/n}\) | \(\dfrac{1}{n}x^{1/n-1}\) |
Bảng đạo hàm cho hàm mũ và logarit
Hàm mũ cơ số \(e\) và cơ số \(a\)
Hàm mũ thường đi kèm biến đổi “nhìn ra” dạng \(e^{u(x)}\) để dùng dây chuyền, vì phần mũ hiếm khi là \(x\) thuần. Bảng Đạo Hàm cho nhóm này cần được dùng cùng việc tính \(u'(x)\) thật cẩn thận, nhất là khi \(u(x)\) là đa thức bậc cao hoặc phân thức. Trong nhiều bài tối ưu, \(e^x\) và \(a^x\) xuất hiện để mô tả tăng trưởng, nên việc đạo hàm chuẩn là bắt buộc.
| Hàm số \(y\) | Đạo hàm \(y’\) |
|---|---|
| \(e^x\) | \(e^x\) |
| \(a^x\) (\(a>0, a\neq 1\)) | \(a^x\ln a\) |
| \(e^{u}\) | \(e^{u}\cdot u’\) |
| \(a^{u}\) | \(a^{u}\ln a \cdot u’\) |
Logarit tự nhiên và logarit cơ số bất kỳ
Với logarit, điều kiện xác định là điểm hay bị bỏ quên: \(\ln x\) yêu cầu \(x>0\). Bảng Đạo Hàm cho \(\ln\) và \(\log_a\) rất dễ áp dụng, nhưng bạn phải nhớ dây chuyền khi gặp \(\ln(u(x))\) hoặc \(\log_a(u(x))\). Một mẹo kiểm tra nhanh là nhìn mẫu số đạo hàm: dạng logarit thường sinh ra \(\dfrac{u’}{u}\).
| Hàm số \(y\) | Đạo hàm \(y’\) |
|---|---|
| \(\ln x\) | \(\dfrac{1}{x}\) |
| \(\ln|x|\) (\(x\neq 0\)) | \(\dfrac{1}{x}\) |
| \(\log_a x\) (\(a>0,a\neq 1\)) | \(\dfrac{1}{x\ln a}\) |
| \(\ln(u)\) | \(\dfrac{u’}{u}\) |
Bảng đạo hàm cho hàm lượng giác
Sin, cos, tan và các hàm liên quan
Nhóm lượng giác thường gây nhầm lẫn dấu, đặc biệt ở \(\cos x\) và các hàm “đảo” như \(\csc x\). Bảng Đạo Hàm giúp bạn khóa chặt các công thức nền, nhưng để tránh sai, hãy luyện thói quen đọc to: “đạo hàm cos là trừ sin”, “đạo hàm tan là sec bình”. Khi gặp \(\sin(u)\) hay \(\tan(u)\), luôn nhân thêm \(u’\) theo dây chuyền.
| Hàm số \(y\) | Đạo hàm \(y’\) |
|---|---|
| \(\sin x\) | \(\cos x\) |
| \(\cos x\) | \(-\sin x\) |
| \(\tan x\) | \(\sec^2 x\) |
| \(\cot x\) | \(-\csc^2 x\) |
| \(\sec x\) | \(\sec x\tan x\) |
| \(\csc x\) | \(-\csc x\cot x\) |
Hàm lượng giác ngược (arcsin, arctan…)
Các hàm ngược lượng giác hay xuất hiện trong bài liên quan tích phân và khảo sát hàm số, nên việc nhớ công thức đạo hàm là lợi thế. Bảng Đạo Hàm cho nhóm này luôn đi kèm căn thức hoặc phân thức, vì vậy bạn cần chú ý điều kiện như \(|x|<1\) với \(\arcsin x\) và \(\arccos x\). Nếu bài có dạng \(\arctan(u)\), hãy nhớ mẫu số thành \(1+u^2\) và nhân \(u’\).
| Hàm số \(y\) | Đạo hàm \(y’\) |
|---|---|
| \(\arcsin x\) | \(\dfrac{1}{\sqrt{1-x^2}}\) |
| \(\arccos x\) | \(-\dfrac{1}{\sqrt{1-x^2}}\) |
| \(\arctan x\) | \(\dfrac{1}{1+x^2}\) |
| \(\operatorname{arccot} x\) | \(-\dfrac{1}{1+x^2}\) |
Mẹo dùng bảng đạo hàm để giải bài nhanh
Quy trình 4 bước khi gặp biểu thức phức
Một quy trình hiệu quả là: (1) rút gọn và đưa về dạng quen thuộc, (2) nhận diện “hàm ngoài – hàm trong”, (3) tra công thức tương ứng, (4) nhân thêm đạo hàm của phần trong nếu có hàm hợp. Bảng Đạo Hàm chỉ là bước (3), còn tốc độ làm bài phụ thuộc nhiều vào bước (1) và (2). Khi luyện tập, bạn nên tự hỏi “điểm khó là biến đổi hay là công thức” để cải thiện đúng chỗ.
Lỗi thường gặp và cách tránh
Sai dấu là lỗi phổ biến nhất, đặc biệt ở \(\cos x\), \(\cot x\) và quy tắc thương, vì chỉ cần nhầm vị trí \(u’v-uv’\) là kết quả sai hoàn toàn. Bảng Đạo Hàm cũng không giúp nếu bạn quên điều kiện xác định, dẫn đến kết luận sai miền hoặc bỏ mất nghiệm hợp lệ. Một cách tự kiểm tra là thay thử giá trị đơn giản (ví dụ \(x=1\)) để xem đạo hàm có “hợp lý về độ lớn và dấu” hay không.
Bài tập mẫu và cách kiểm tra kết quả
Ví dụ 1: Đạo hàm hàm hợp điển hình
Xét \(y=\ln(2x^2+1)\), ta nhận ra hàm ngoài là \(\ln(\cdot)\) và hàm trong là \(u=2x^2+1\). Bảng Đạo Hàm cho \(\ln(u)\) là \(y’=\dfrac{u’}{u}\), nên \(u’=4x\) và \(y’=\dfrac{4x}{2x^2+1}\). Khi kiểm tra, bạn thấy với \(x>0\) thì \(y’>0\), phù hợp trực giác “log của biểu thức tăng” trong vùng đó.
Ví dụ 2: Tiếp tuyến và tối ưu cơ bản
Cho \(y=x^3-3x+2\), đạo hàm là \(y’=3x^2-3\) và giải \(y’=0\) được \(x=\pm 1\) để xét cực trị. Bảng Đạo Hàm cho \(x^n\) giúp tính nhanh và tránh nhầm lẫn hệ số, đặc biệt khi đa thức dài hơn. Nếu cần tiếp tuyến tại \(x=1\), bạn có hệ số góc \(y'(1)=0\) nên tiếp tuyến là đường thẳng song song trục hoành tại shop Vape.
Tổng kết và gợi ý ôn tập hiệu quả
Học thuộc có chọn lọc và luyện nhận dạng dạng hàm
Bạn không nhất thiết học thuộc tất cả công thức ngay từ đầu, nhưng nên nắm chắc nhóm đại số, mũ–logarit và lượng giác cơ bản. Bảng Đạo Hàm sẽ trở thành “bản đồ” học tập nếu bạn luyện theo hướng nhận dạng nhanh dạng hàm và luôn kèm bước dây chuyền khi có hàm hợp. Khi ôn thi, hãy dành thời gian làm bài tổng hợp (có biến đổi + quy tắc) để kỹ năng tra bảng chuyển thành phản xạ.
