Công Thức Đạo Hàm là nền tảng quan trọng của giải tích, giúp bạn tính tốc độ thay đổi và xử lý nhiều bài toán khảo sát hàm số. Khi nắm chắc các quy tắc và bảng đạo hàm cơ bản, bạn sẽ rút ngắn thời gian biến đổi và hạn chế sai sót khi làm bài. Bài viết này tổng hợp hệ thống công thức thường gặp, kèm ví dụ và mẹo áp dụng hiệu quả.
Công Thức Đạo Hàm là gì và dùng để làm gì?
Công Thức Đạo Hàm mô tả cách tính đạo hàm của một hàm số theo biến, thường ký hiệu là y’ hoặc f'(x). Đạo hàm phản ánh mức độ thay đổi tức thời của hàm số, vì vậy nó xuất hiện nhiều trong khảo sát đồ thị, tìm cực trị, xét đơn điệu và tối ưu hóa. Trong thực tế, đạo hàm còn liên quan đến vận tốc, gia tốc, tốc độ tăng trưởng, và nhiều mô hình kinh tế – kỹ thuật.
Để dùng tốt, bạn cần hiểu đạo hàm không chỉ là “công thức bấm ra kết quả” mà là một ngôn ngữ biến đổi. Khi gặp bài toán, hãy xác định dạng hàm (tổng, tích, thương, hợp) để chọn đúng quy tắc. Việc phân loại đúng từ đầu thường giúp bạn tránh nhầm lẫn và tiết kiệm rất nhiều bước.
Ký hiệu và điều kiện cơ bản
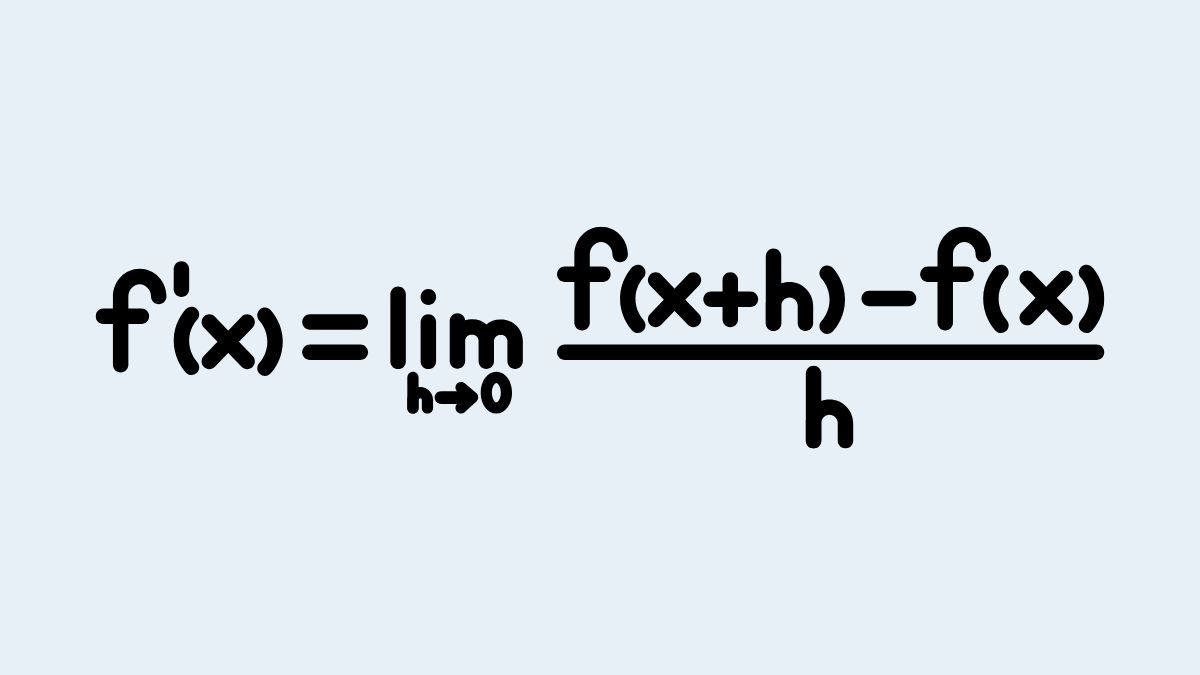
Đạo hàm tại điểm x0 tồn tại khi giới hạn theo định nghĩa tồn tại và hữu hạn. Trong chương trình phổ thông, bạn thường thao tác với các hàm quen thuộc nên điều kiện tồn tại ít khi làm khó, nhưng vẫn cần lưu ý miền xác định. Nếu hàm có căn, mẫu, hoặc logarit, hãy kiểm tra điều kiện trước khi biến đổi.
Bạn cũng nên thống nhất ký hiệu ngay từ đầu: y = f(x) thì y’ = f'(x). Với hàm nhiều bước, việc viết rõ “đặt u = …” giúp giảm lỗi khi dùng quy tắc dây chuyền. Thói quen trình bày mạch lạc đặc biệt hữu ích trong các bài khảo sát dài.
Công Thức Đạo Hàm các quy tắc tính nhanh cần nhớ
Công Thức Đạo Hàm thường được áp dụng qua các quy tắc tính nhanh, giúp bạn xử lý các biểu thức phức tạp mà không cần quay lại định nghĩa. Bạn nên thuộc nhóm quy tắc cốt lõi, sau đó luyện bài để phản xạ tự nhiên khi gặp dạng tương ứng. Dưới đây là các quy tắc phổ biến nhất trong bài tập.
Quy tắc tuyến tính: tổng, hiệu và nhân với hằng số

Nếu y = u ± v thì y’ = u’ ± v’. Nếu y = k·u (k là hằng số) thì y’ = k·u’. Đây là quy tắc xuất hiện nhiều nhất vì hầu hết hàm số đều là tổ hợp của các thành phần nhỏ. Khi triển khai, hãy tách hàm thành các “mảnh” đơn giản để đạo hàm nhanh và gọn.
Lưu ý quan trọng là bạn chỉ được “kéo” hằng số ra ngoài, không được kéo biến số ra như hằng số. Khi biểu thức có dấu ngoặc, hãy giữ nguyên cấu trúc rồi đạo hàm từng phần để tránh bỏ sót dấu âm. Thực hành nhiều sẽ giúp bạn giảm lỗi trình bày và sai hệ số.
Quy tắc tích và quy tắc thương
Nếu y = u·v thì y’ = u’·v + u·v’. Nếu y = u/v (v ≠ 0) thì y’ = (u’·v – u·v’) / v^2. Hai quy tắc này đặc biệt hữu ích khi gặp đa thức nhân lượng giác, hoặc phân thức hữu tỉ. Trong làm bài, bạn nên viết u, v rõ ràng trước khi thế vào công thức để tránh đảo dấu.
Một mẹo nhỏ là kiểm tra nhanh bằng “đơn vị dạng”: mẫu của quy tắc thương luôn là v^2. Nếu bạn thấy mẫu không bình phương, khả năng cao bạn đã viết sai. Với quy tắc tích, hãy đảm bảo đủ hai hạng tử và không quên nhân lại với phần còn nguyên.
Quy tắc dây chuyền cho hàm hợp

Nếu y = f(g(x)) thì y’ = f'(g(x))·g'(x). Quy tắc này là chìa khóa cho các hàm có dạng mũ, log, lượng giác đi kèm biểu thức trong ngoặc như sin(2x-1), e^(x^2), ln(3x+2). Khi áp dụng, bước “đặt u” giúp bạn nhìn ra cấu trúc và đạo hàm chuẩn.
Bạn nên ưu tiên quy tắc dây chuyền thay vì khai triển phức tạp, vì khai triển dễ dẫn đến sai sót và dài dòng. Sau khi đặt u, hãy đạo hàm theo u trước rồi nhân u’. Cách làm này nhất quán, đặc biệt hiệu quả trong các bài tối ưu hóa và khảo sát hàm số.
Công Thức Đạo Hàm bảng đạo hàm các hàm cơ bản
Công Thức Đạo Hàm không thể thiếu bảng đạo hàm các hàm cơ bản, vì đây là “từ vựng” để bạn ghép vào quy tắc. Nếu chưa thuộc, bạn nên học theo cụm: đa thức – mũ – log – lượng giác. Khi đã thuộc bảng, phần còn lại chỉ là chọn đúng quy tắc và biến đổi gọn.
Đạo hàm lũy thừa, căn và đa thức
Với y = xn (n là số thực), y’ = n·x(n-1) (trong phạm vi phù hợp miền xác định). Trường hợp y = √x = x^(1/2) thì y’ = 1/(2√x) với điều kiện x > 0. Với đa thức, bạn chỉ cần áp dụng quy tắc tuyến tính và công thức lũy thừa cho từng hạng.
Khi gặp phân thức kiểu 1/x = x^(-1), việc chuyển về lũy thừa âm thường giúp đạo hàm nhanh: (x^(-1))’ = -x^(-2) = -1/x^2. Tuy nhiên, đừng quên điều kiện x ≠ 0 trước khi rút gọn. Kiểm soát miền xác định giúp bạn tránh kết luận sai trong khảo sát.
Đạo hàm hàm mũ và logarit
Với y = ex thì y’ = ex. Với y = ax (a > 0, a ≠ 1) thì y’ = ax·ln(a). Với y = ln(x) thì y’ = 1/x (x > 0), và y = log_a(x) thì y’ = 1/(x·ln(a)). Nhóm công thức này thường đi kèm quy tắc dây chuyền khi biến x được thay bằng biểu thức.
Một lỗi hay gặp là quên ln(a) khi đạo hàm ax, hoặc nhầm ln(x) với log_a(x). Bạn nên ghi nhớ: ex “giữ nguyên”, còn a^x luôn kéo theo ln(a). Khi gặp ln(g(x)), hãy nhớ kết quả dạng g'(x)/g(x) để viết nhanh và đúng.
Đạo hàm lượng giác cơ bản
Các công thức thường dùng gồm: (sin x)’ = cos x, (cos x)’ = -sin x, (tan x)’ = 1/cos2 x, (cot x)’ = -1/sin2 x. Khi biến là g(x) thay vì x, bạn nhân thêm g'(x) theo quy tắc dây chuyền. Phần dấu âm của cos và cot là nơi dễ nhầm nhất.
Trong bài khảo sát, các biểu thức lượng giác thường đi kèm phân thức hoặc tích, nên bạn sẽ phải kết hợp nhiều quy tắc cùng lúc. Khi làm, hãy xác định “lõi lượng giác” trước, sau đó mới xử lý phần bao quanh. Cách này giúp bạn không bỏ quên dấu và hệ số trong ngoặc.
Công Thức Đạo Hàm: ví dụ minh họa áp dụng quy tắc
Công Thức Đạo Hàm sẽ dễ nhớ hơn nếu bạn nhìn qua một số ví dụ điển hình. Ở mỗi ví dụ, mục tiêu là nhận diện cấu trúc: tổng – tích – thương – hàm hợp. Khi xác định đúng cấu trúc, các bước còn lại chỉ là thay công thức và rút gọn hợp lý.
Ví dụ 1: Hàm đa thức và phân thức đơn giản
Xét y = 3x4 – 5x + 2. Ta có y’ = 12x3 – 5 vì đạo hàm từng hạng theo quy tắc lũy thừa và hằng số. Đây là dạng cơ bản nhất, thường xuất hiện trong bước xét đơn điệu hoặc tìm cực trị của hàm đa thức.
Xét tiếp y = 1/x + √x. Viết lại y = x^(-1) + x^(1/2), suy ra y’ = -x^(-2) + (1/2)x^(-1/2) = -1/x^2 + 1/(2√x). Bạn nên rút gọn ở mức vừa đủ để tránh sai số đại số không cần thiết.
Ví dụ 2: Tích và thương có lượng giác
Xét y = x2·sin x. Đặt u = x2, v = sin x thì y’ = 2x·sin x + x^2·cos x. Dạng này rất phổ biến trong bài tính đạo hàm và cũng thường dùng để xét dấu của y’ khi khảo sát.
Xét y = (sin x)/x. Đặt u = sin x, v = x thì y’ = (cos x·x – sin x·1)/x2 = (x cos x – sin x)/x2. Khi viết kết quả, bạn cần giữ mẫu x^2 và không quên điều kiện x ≠ 0 từ ban đầu.
Ví dụ 3: Hàm hợp với mũ và logarit
Xét y = e^(x2+1). Đặt g(x) = x2+1, suy ra y’ = e^(x^2+1)·(2x). Đây là ví dụ mẫu của quy tắc dây chuyền với hàm mũ, thường gặp trong bài tối ưu hóa và khảo sát.
Xét y = ln(3x-2). Ta có y’ = (3)/(3x-2) vì (ln g(x))’ = g'(x)/g(x). Bạn nên ghi kèm điều kiện 3x-2 > 0 để hoàn chỉnh lời giải, đặc biệt khi bài yêu cầu xét miền xác định hoặc giải bất phương trình liên quan.
Công Thức Đạo Hàm: mẹo ghi nhớ và tránh lỗi thường gặp
Công Thức Đạo Hàm sẽ trở nên “nhẹ” hơn nếu bạn có chiến lược học và kiểm lỗi. Thay vì học rời rạc, hãy gom công thức theo nhóm và luyện bài theo từng dạng. Mỗi lần sai, bạn nên ghi chú lỗi thuộc nhóm nào: dấu âm, thiếu hệ số, quên nhân đạo hàm trong ngoặc, hoặc nhầm quy tắc.
Cách học theo nhóm và luyện phản xạ
Bạn nên chia công thức thành 4 cụm: lũy thừa–căn, mũ–log, lượng giác, và quy tắc biến đổi (tuyến tính, tích, thương, dây chuyền). Sau đó, mỗi ngày luyện 10–15 bài ngắn, mỗi bài chỉ tập trung một dạng, trước khi chuyển sang bài phối hợp. Cách luyện này giúp bạn hình thành phản xạ nhận dạng dạng hàm rất nhanh.
Khi đã quen, hãy luyện các bài phối hợp: ví dụ tích của đa thức và lượng giác, hoặc logarit của phân thức. Mục tiêu là không chỉ ra đáp án đúng mà còn trình bày gọn, ít bước thừa. Thói quen viết “đặt u = …” trong các hàm hợp giúp bạn hạn chế sai sót đáng kể.
Kiểm lỗi nhanh trước khi chốt đáp án
Với quy tắc thương, hãy kiểm tra mẫu có bình phương hay chưa, vì đây là lỗi phổ biến. Với lượng giác, hãy đặc biệt chú ý dấu âm của (cos x)’ và (cot x)’. Với hàm hợp, bạn hãy rà lại xem đã nhân thêm đạo hàm “bên trong” hay chưa, nhất là trong e^(g(x)) và ln(g(x)) tại Mua Vape ở đâu.
Cuối cùng, bạn có thể kiểm tra sơ bộ bằng cách thay một giá trị đơn giản vào biểu thức đạo hàm để xem có hợp lý về dấu và độ lớn không. Cách kiểm này không thay thế lời giải, nhưng giúp phát hiện nhanh các lỗi hiển nhiên. Khi làm bài thi, một lần kiểm nhanh như vậy có thể cứu bạn khỏi những sai sót đáng tiếc.
